- September 30, 2022
- Posted by: Shane Daly
- Category: Trading Article

If you’re an options trader, then you know that the delta, gamma, and theta of your position are referred to as the “Greeks.” But what exactly are the Option Greeks and why do they matter to your option price?
Options Greeks are a way to measure an option’s sensitivity to ever-changing external factors. Here’s a more detailed look at three of the Option Greeks that we find important.
3 Options Greeks To Know
The three Option Greeks that we find most important are delta, gamma, and theta. Each one measures and impacts a different aspect of your position and how it might change over time.
What is Delta?
Delta is a measure of how much an option’s price will change in relation to a change in the price of the underlying asset.
For example, let’s say you own a call option on XYZ stock with a delta of 0.50. This means that for every $1 move in XYZ’s stock price (up or down), your option will gain or lose $0.50 ($50.00) in value. So, if XYZ stock goes up $1, your call option will increase in value by $0.50. Conversely, if XYZ stock goes down $1, your call option will decrease in value by $0.50.
It’s important to note that delta values can range from 0 to 1 for calls (0 to -1 for puts). A call with a delta of 0 is insensitive to changes in the underlying asset’s price and will not move at all no matter how much the underlying asset’s price changes. A call with a delta of 1 (or -1 for puts) is completely sensitive to changes in the underlying asset’s price and will move dollar-for-dollar with the underlying asset.
Let’s put this into general practice and looking at the $42.50 strike price for a call, we will use the Delta of .6019 (.60) and let’s say the underlying price is $42.50.
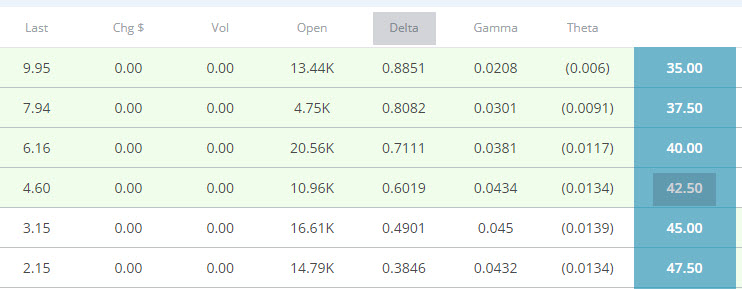
If the stock price goes to $43.50 (+1.00), the value of this option contract will go up to $60.00 (.60 X 100 shares). Note that the green background represents ITM options and have a higher Delta due to the intrinsic value of those options.
If this was a put option (imagine the Greeks are the same) and the underlying went down $1.00, you’d also make $60.00
Why Delta Matters When Trading Options
Now that you know what delta is and how it works, you’re probably wondering why it matters. After all, can’t you just look at an option’s price and get a pretty good idea of how sensitive it is to changes in the underlying asset’s price?
While that’s true to some extent, deltas can give you a more accurate picture because they account for things like time decay and changes in volatility that can impact an option’s price.
As you get closer to expiration, the Delta will not be as high as an expiration date that is further out. When you get closer to expiration, the next two Greeks will have a larger impact.
What is Gamma?
Gamma is the rate of change of delta for every $1 change in the underlying price of the asset. Gamma represents the acceleration (think fuel on a fire) at which an option’s price increases or decreases. Think of gamma as being what the next dollar move is.
In its simplest form, gamma measures an option’s sensitivity to changes in the underlying asset’s volatility. A high-gamma position will be more sensitive to changes in volatility than a low-gamma position.
We will use the same example as the Delta section: The first $1.00 up in the underlying makes $60.00. The Gamma is going to increase that with the next $1.00 move up.
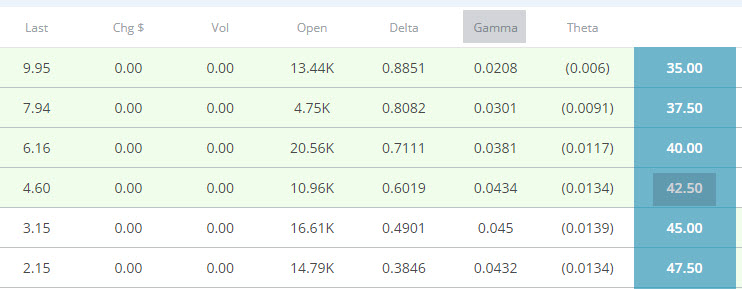
The stock price now goes from $43.50 to $44.50. The Delta pays you another $60.00 but now we get the acceleration with Gamma that pays you an extra $4.00 (.0434 x 100)
The first $1.00 increase in the underlying: $60.00
The second $1.00 increase: $60.00 + $4.00 = $64.00
Total for a $2.00 move up in the underlying stock: 60+60+4 = $124.00 increase in the value of the contract.
The same is true to the downside if your underlying is going down in price. A $2.00 drop in the underlying will lose you $124.00 of value.
Gamma risk increases the closer we get to expiration and can help or hurt us depending on our position. If we’re in an options position that is out of the money, the Gamma risk can allow us to recover much faster if the stock or ETF turns around and starts to move in our favor.
If you’re in an options position and that stock moves very quickly in your favor, the Gamma is going to help you make more money.
How Theta Works
Theta is what is referred to as time decay and is measured in dollars and cents per day. For example, let’s say you own a call option on XYZ stock with a theta of -0.10. This means that for every day that passes, your option will lose $10 (remember, contracts contain 100 shares of underlying) in value. The clock starts ticking the moment you enter an options trade.
Theta is one of the “Greeks” because it is used to gauge the sensitivity of an options contract to changes in one of the factors that affect an options price: time (extrinsic value)
The effect of theta is most pronounced in the last few days before expiration. That’s because there are fewer and fewer days remaining in which the underlying asset can move enough to offset the time decay. As expiration gets closer, theta becomes more negative and you will begin to lose more money each day.
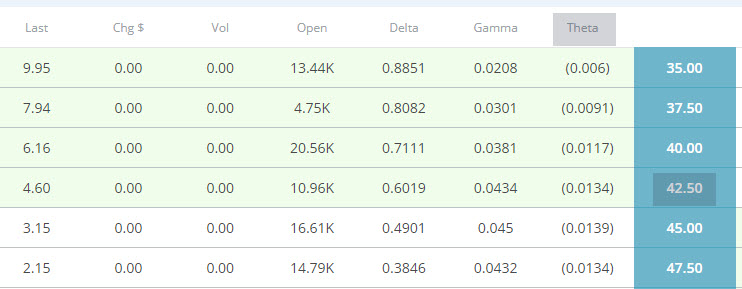
Back to our real life example using the same strike price of $42.50. The Theta is -.0134 which means that every day, the value of this contract will decrease by $1.34 regardless of how strong the underlying instrument is.
Other Greeks
Other Greeks include Vega (sensitivity to changes in volatility), and Rho (sensitivity to changes in interest rates).
Conclusion:
This was an introduction to the Greeks and how they can help you better understand your options and positions. Remember, each Greek represents a different factor that can affect the price of an options contract. By understanding how each Greek works, you can make more informed decisions about your options trades.
Greeks are dynamic and will change over the course of the life of the contract. The Greeks won’t make or break your Options trading success but we do find the most important aspect is the effect of time decay on our positions as well as the volatility of our underlying instrument.
At Netpicks, we generally look at trading in-the-money options with at least 20-40 days of expiration. We do this so our contract has value the moment we buy and get a lower Theta as we wait for the underlying to make the move.

